引子
DES 提出的时候,由于 S 盒来历不明,以及传说 NSA 唆使 IBM
公司把有效密钥长度从 64 位减少到 56 位,DES 被怀疑有 NSA
留下的后门。直到上世纪 90 年代,
“差分密码攻击”被公开提出,相关质疑终于消解 —— DES 的 S
盒,恰到好处地提供了对差分密码攻击的超强防御能力;而如果采用随机的 S
盒,抗差分密码攻击的能力则大大减弱
事实上,IBM 的研究员们早在 70
年代就已经发现了差分密码攻击方法,并针对此攻击方式特殊构建了 S
盒。出于国家安全的考虑,NSA 要求 IBM
保守秘密,于是差分密码攻击方法在二十余年后才得以重新被其他人发现
关于DES
原理分析
1945年,Shannon
提出了设计密码体制的两种基本方法——混淆(confusion)、扩散(diffusion)
- 混淆: 使密文与密钥之间的关系变得复杂
一个优秀的密码系统,应该很难通过几组密文推断出密钥的特征
- 扩散:使明文与密文的关系变得复杂。
常常体现为:明文的任何一个bit的变动,都会对密文产生翻天覆地的变化。
比如针对 Many-Time-Pad
的攻击。这种攻击就是利用了“明文的异或等于密文的异或”这种特征,使得攻击者轻易地得到了明文的大量统计信息,帮助攻击者攻破密码体系
实际操作中一些非线性的操作可以实现“混淆”。例如乘法(乘法对二进制位有很复杂的改变。回顾一下《数字逻辑》,一个乘法器需要大量的逻辑门才能实现)、S盒(Substitution-box,替换盒。就是一个特定的函数,其映射关系是精心设计以对抗攻击的)
因此,对于线性元件与非线性元件。线性,联系一下函数,即可以一一对应上,比如只是简单的异或,那么我们拥有一组明密文对时,就可以轻易解出密钥。之所以分组密码具有安全性,是因为存在非线性元件
至于对“扩散”的实现,一般采用线性变换、置换、循环移位等手段。多次迭代可以大大增强混淆和扩散的强度,使密文、明文、密钥之间的关系异常复杂,以至于攻击者极其难以分析
算法
这里简单回顾一下DES的算法。简要来说,整个算法分为两大部分:迭代加密(左边的16轮加密)与密钥调度(右边生成16个子密钥)
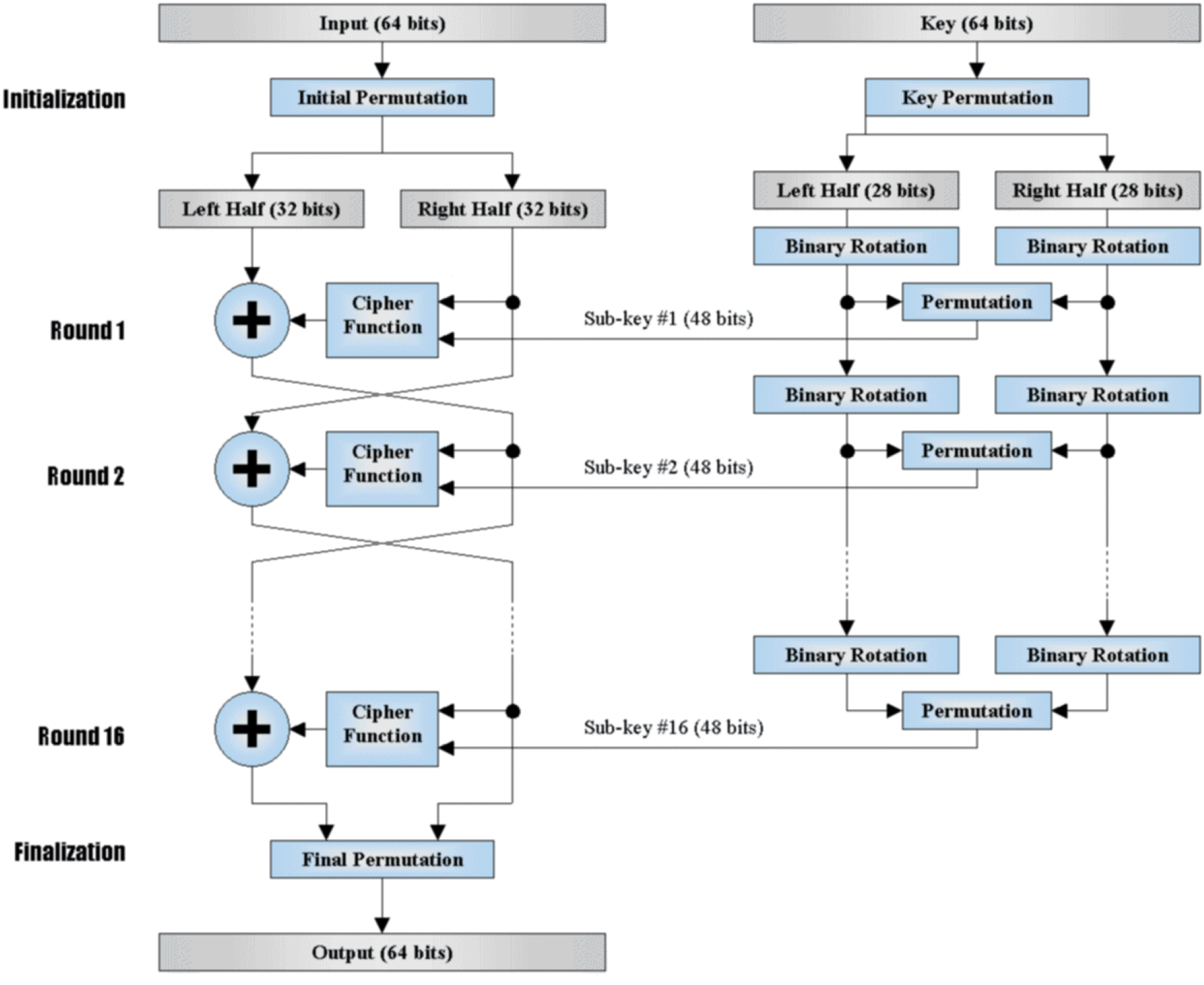
1. 从 64-bit 的主钥匙里面选取特定的 56
位,其余的位就没用了。于是我们现在手上有了一个 56
位的布尔数组。把它分成左、右两个半密钥,它们都是 28-bit 的布尔数组
2.
左、右两个半密钥都左旋(也就是循环左移。整个数组往左移,左边弹出去了的东西补到最右边去)一定位数,这个左移的位数也是指定的。有些轮次是
1 位,有些轮次是 2 位
3.
把左、右半密钥拼起来,再做一个置换,就得到了这一轮生成的子密钥。这个置换是从
56-bit 的数组里面选取指定的 48 位。所以现在每一轮都可以生成一个 48
位的子密钥。(注意,步骤 3 并不改变左右半密钥)
4. 重复 步骤 2、步骤 3 一共 16 次,于是得到了 16 个 48-bit 的子密钥
得到16把子密钥后,便用这些开始加密
- 输入的明文(长度为 64 的布尔数组)做一个置换(IP置换)。仍然得到
64-bit 的数组(不然就丢失信息了!)
- 把得到的数组拆成左、右两半边。每边是 32 位长度
- 每一轮迭代,都是接收一组 L, R,返回 L', R' ,作为下一轮迭代的 L, R .
迭代过程如下:
\[ L' = R\\ R' = L \bigoplus F(R,subkey) \] 其中F函数(称为轮函数)是整个算法的核心,功能是:以一个子密钥,加密 32-bit 的信息
- 利用之前得到的 16 个子密钥,执行步骤 3 一共 16 次
- 将最终的 R 与 L 拼接,再做一次置换(FP置换),即得到密文
DES的破解之路
如今DES变得不再安全,很大程度得益于当今计算水平的不断提高。而从穷举搜索到差分分析,中间也是有无数科学家贡献了他们的智慧
| 相关人物 | 方法 | 原理 | 可行性 | | ----------------- |
-------------------------------------- |
------------------------------------------------------------------------
|
-------------------------------------------------------------------------------
| | Diffie Hellman | 并行计算机上进行整个密钥空间的穷举搜索 |
建造一个每微秒可以搜索一个密钥的VLSI芯片,以百万个这样的芯片构建搜索机器
| 时间为\(10^5s\),大约一天机器成本2000万美元,每个解成本5000美元
| | Hellman | 基于时间-内存权衡的选择明文攻击 |
使用更多的内存来减少解密所需的时间,通过预处理以提高破解效率 |
时间上每天产生100个解,同一台机器2.3年;机器成本500万美元,每个解成本1到100美元
| | Schaumuller-Bichl | 形式解码方法 |
找到每个密文位的形式表达式,作为明文位和密钥位的位乘积的异或和 |
需要大量的时间成本,使得本方法不可能 | | Chaum Evertse | 中间相遇攻击 |
通过在中间阶段获取部分信息,从而有效地减少密钥搜索的工作量 |
轮数小于八轮时有效 | | Davies | 线性分析 |
利用相邻S盒输出的相关性,产生16个密钥位之间的线性关系 |
已接近实用性的边缘 |
差分分析
简单的举例
如对于线性元件\(c = p \bigoplus k\),其中,c是密文,p是明文,k是密钥。此时当我们有一对密文对时,就可以得到一对明文对。\[c_0 \bigoplus c_1 = (p_0 \bigoplus k_0)\bigoplus(p_1 \bigoplus k_1)\] 通过这种⽅式,我们可以从⼀对密⽂中直接得到⼀对明⽂的异或,经过⼀次异或运算消除了密钥。这体 现了差分攻击的思想,我们可以不从单个明⽂和密⽂中考虑信息的获取,⽽是从⼀对密⽂和⼀对明⽂的 差分⼊⼿,进⾏破解。
原理分析
通过分析特定差分对(一对明文之间的差异)对应的密文差分(一对相应密文之间的差异)的影响来提取密钥。
差分攻击的效力依赖于两个方面:混淆和扩散。如果密码系统在处理相同差分对的情况下产生了高度非随机的密文差分,攻击者更容易推断出密钥。因此,设计密码系统时需要注意确保混淆和扩散的均衡,以增强系统的安全性。
攻击流程
明文选择和初始差分: 选择明文差分对,计算初始差分。
第四轮函数输入和输出差分: 利用密文对,得到第四轮函数的输入差分。通过拓展变换和轮密钥加操作,获得输出差分。
差分传播: 利用S盒的扩散特性和拓展变换,传播差分到第四轮后的S盒输出。对S盒的输出差分进行分析,求解部分轮密钥。
轮密钥穷举: 对每个S盒的轮密钥进行穷举,与已知的输出差分比较,得到候选轮密钥集合。
求解完整轮密钥: 利用密钥拓展算法,将部分轮密钥还原成完整的48位轮密钥。
密钥还原: 利用P盒还原56位初始密钥,然后根据轮密钥生成算法,还原最初的密钥。
验证和优化: 使用明文密文对进行加密,验证得到的密钥是否正确。若不一致,回到步骤2。
代码示例
这里通过一个简单的python代码体会一下差分分析攻击的流程。
s=[[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
[0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
[4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]]
def functions(key):
'''
s盒代替
'''
return_list=''
row=int( str(key[0])+str(key[5]),2)
raw=int(str( key[1])+str(key[2])+str(key[3])+str(key[4]),2)
return_list+=changtos(s[row][raw],4)
return return_list
# 模拟DES的S盒代替运算。它将输入的6位二进制数按照特定规则映射到4位二进制数。具体映射规则存储在S盒 s 中
def changtos(o,lens):
'''
二进制转换
'''
return_code=''
for i in range(lens):
return_code=str(o>>i &1)+return_code
return return_code
# 将S盒代替的结果转换成二进制形式
def codeyihuo(code,key):
'''
异或运算
'''
code_len=len(key)
return_list=''
for i in range(code_len):
if code[i]==key[i]:
return_list+='0'
else:
return_list+='1'
return return_list
# 将输入的两个二进制字符串进行异或操作,返回结果
b=''
d=''
a=[]
c=[]
for i in range(64):
b+=str(functions(str('{:06b}'.format(i))))
d+=str(functions(str(codeyihuo('{:06b}'.format(i),'000001'))))
#print('b['+str(i+1)+']:'+b)
#print('d['+str(i+1)+']:'+d)
a.append(str(codeyihuo(b[i*4:i*4+4],d[i*4:i*4+4])))
#print('a:'+str(a))
# 通过循环遍历64个输入,得到S盒代替的结果 b 和 d,然后计算它们的异或结果,存储在列表 a 中
for i in range(16):
number=0
c.append(str('{:04b}'.format(i)))
for j in range(len(a)):
if a[j]==c[i]:
number+=1
print('输出差分'+str(c[i])+'数量为'+str(number)+'个')
# 遍历16个可能的差分,统计列表 a 中有多少个与每个差分相匹配的情况运行结果:
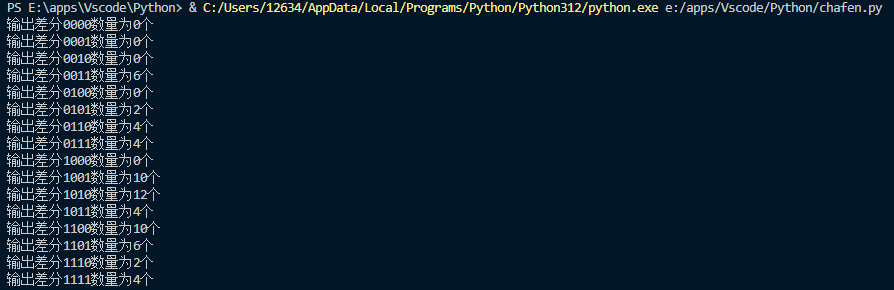
结语
差分分析依赖于密文对和明文对之间的差异,寻找具有特定差分特性的密文对。尽管差分分析在一些密码体制中可能有效,但它的成功程度很大程度上取决于密码算法的设计,特别是S-盒的结构。DES的S-盒经过优化,具有一定的抗击差分分析的能力
分组加密的轮数对于差分分析的影响也很显著。DES使用的轮数是一个关键因素,8轮DES可以在短时间内受到差分分析的威胁,而16轮DES则显著增加了攻击的难度。增加轮数对差分分析和穷尽密钥搜索的效率有着不同的影响,这是一个需要权衡的设计考量
尽管差分分析在理论上是可行的,但由于需要大量的时间和数据支持,它在实际应用中并不实用。因此,在设计密码算法时,除了考虑理论攻击外,还需要关注实际可行性和性能方面的问题。密码学的发展需要不断提高密码算法的抗击各种攻击手段的能力,以确保信息安全性
